El taller ludicomatemático de este sábado 27 de mayo tuvo un sentido especial. Como ya lo hemos hecho en años anteriores, participamos del Día de los Patrimonio 2023, con la misión de realizar el aporte cultural de esta ciencia y su actividad desde nuestro territorio. ¡Gracias a todas las personas que aceptaron la invitación!

Desde el año 2018 se instaura esta fecha conmemorativa en honor a la matemática iraní Myrna Mizarkhani. A continuación, detallamos el por qué conmemoramos este 12 de Mayo el trabajo cientifico de las mujeres matemáticas:

El 12 de mayo de 1977 es la fecha de nacimiento de Maryam Mirzakhani.

¿Quién es Maryam Mirzakhani?

Maryam Mirzakhani fue una matemática iraní y profesora de matemáticas en la Universidad de Stanford. Fue una de las principales expertas mundiales en geometría y sistemas dinámicos. Sus hermosos y asombrosos resultados y su vida y carrera son una inspiración para todos, mujeres y hombres, para perseguir sus sueños en la ciencia. Murió trágicamente de cáncer en 2017 a la temprana edad de 40 años.

En 2014, Maryam Mirzakhani recibió la Medalla Fields por sus destacadas contribuciones a la dinámica y la geometría de las superficies de Riemann y sus espacios de módulos, convirtiéndose en la primera mujer y la primera iraní en ser reconocida por sus logros matemáticos por este importante premio matemático.

En las pocas entrevistas que concedió, Mirzakhani habló con elocuencia de la belleza de las matemáticas y su alegría al hacerlas.

El 12 de mayo, su cumpleaños, fue elegido para celebrar Mujeres en las Matemáticas en su memoria.

Referencias

• May12.org
• Mujeres con ciencia (Perfil Myriam Mizhankani)

Un principio fundamental del trabajo que realizamos cada jornada, es promover el trabajo y resolución de problemas de forma colaborativo, integrando estudiantes de distintos niveles de escolaridad y colegios de procedencia. Nos parece que es importante disponer de instancia en que esas distintas realidades se encuentren en un escenario no competitivo, pero fuertemente reflexivo. Esa es nuestra contribución a niñas, niños y jovenes que están buscando una instancia de explorar su sentido científico y matemático.

Durante este año hemos participado del diseño y propuesta de Modelo de Gestión Territorial de Divulgación y Comunicación Científica. A partir del trabajo realizado durante estos años, hemos avanzado en visibilizar el trabajo sostenido en el ámbito de cultura, entendida también constituida a través del quehacer científico. El fin último de esta iniciativa en propiciar de parte 9la comunidad ciudadana el justo reconocimiento y relevancia del quehacer científico y como este permea sus vidas. En este esfuerzo conjunto entre la Universidad de Los Lagos y la Ilustre Municipalidad de Osorno, se han sumado un grupo de académicas, académicos interesados en constituir este vínculo directo con la ciudadanía a través del trabajo conjunto con el gobierno local.

Mayores Antecedentes:

• Modelo de Gestión Territorial de Divulgación y Comunicación Científica (Presentación)
• Consejo Asesor Científico: El desafío de llevar la ciencia a toda la comunidad (Universidad de Los Lagos)
• Conformación del Consejo Asesor Científico que apoyará nuestro Museo Interactivo (Corporación Cultural de Osorno)

Hemos estado trabajando intensamente, a veces silenciosamente, pero siempre con nuestro norte al frente. Por estos días hemos canalizado el trabajo a través de la plataforma instragram, aprendiendo a caminar en este nuevo canal de comunicación! Síguenos!

Como cada sábado, continuamos nuestro trabajo de abrir una ventana, una mirada matemática para comprender nuestro alrededor. Puedes informarte de nuestro trabajo también desde la página del Museo Interactivo de Osorno!

Durante la jornada del día sábado 28 de Mayo, nos súmanos a las distintas actividades que a nivel nacional se realizaron como parte del Dïa Nacional del Patrimonio. Nuestra jornada fue especial, compartimos nuestra visión de que la matemática es un patrimonio universal, que no obedece a fronteras idiomáticas, que emergió como una expresión del espíritu humano, de su curiosidad por entender las relaciones y patrones presentes en la naturaleza.

Por segundo año consecutivo participaremos del día del patrimonio que organiza el Ministerio de Cultura, Las Artes y El Patrimonio. Esta es una forma de reconocer el trabajo matemático como un proceso creativo, artístico, universal, y que es patrimonio de la humanidad pasada, presente y futura.

Mas detalles: Enlace Plataforma Día del Patrimonio 2022

La semana pasada participamos en el programa 'En Pauta' del canal Osorno TV más, donde presentamos el trabajo que realizaremos durante los talleres ludicamatemático cada día sábado en el Museo Interactivo de Osorno

Entrevista en Extenso: Desde minuto 49:59

Durante el mes de Abril se realizará las XXXIV Jornadas de la Matemática Zona Sur, congreso de carácter nacional que en esta oportunidad es organizado por el Departamento de Ciencias Exactas de la Universidad de Los Lagos. Compartimos algunas referencias importantes:

1. Página We XXXIVJMZS
2. Formulario de Inscripciones (Hasta el 15 de Abril)

El congreso al ser en modalidad virtual es de carácter gratuito, incluye conferencias plenarias, cursillos y sesiones científicas. En el diseño del afiche se contó con la autorización del artista venezolano Rafael Araujo, destacado arquitecto y autodidacta. 

Este pasado jueves participamos con una comunicación breve en el contexto de la sesión sobre 'Transición entre la secundaria y la universidad: Resolución de problemas, tecnología e inclusión'. En esta oportunidad, contamos las experiencias, reflexiones y expectativas sobre el trabajo realizado durante los años de ejecución del Círculo Matemática Kimche, entre los énfasis presentados estuvo la urgencia por abordar desafíos existentes al día hoy, tales como brechas sociales, culturales desde espacios inclusivos.

Presentación: Círculo Matemático: Resolución de Problemas como una oportunidad de integración social

¿Cómo atrapar la semilla de un Hualle (Roble), Coigue, Lenga? pequeñas casi imperceptibles en medio del bosque, ¿cómo podemos atraparlas, seleccionarlas con el propósito de repoblación del bosque nativo? El diseño de un atrapa semilla tiene algo de arte, algo de geometría, un buen punto de partida es inspiramos en la geometría de pesos invertidos de Gaudi, o en las superficies de las techumbres de los estadios de Frei Otto. 

Durante el viernes 17 de diciembre participamos de la sesión de 'Matemáticas y Sociedad' como parte del encuentro anual de la Sociedad de Matemática de Chile (SOMACHI), donde compartimos la experiencia en la implementación y desarrollo del curso 'Ludomatemática' que se oferta semestralmente en la parrilla del Centro de Formación Integral de la Universidad de Los Lagos.  En este curso hemos plasmado muchas de nuestras experiencias a lo largo de los más de cinco años frente al Círculo Matemático Kimche, acuñamos algunas frases que nos representan en nuestra acción formativa y de divulgación científica.

• Matemáticas para tod@s
• Conocimiento como un juego, juego es conocimiento
• Ciencia ciudadana, ciudadanos científicos.

Presentación “Ludomatemática" ‘Matemática como aporte a la formación integral’

Agradecemos el reconocimiento y visibilización desde la Red de Divulgación Matemática de Chile (DIMATCHILE) al considerarnos como parte de las acciones de divulgación matemática existentes en Chile. Desde el sur, renovamos nuestro compromiso en compartir toda la matemática que podamos contar!

Compartimos la convocatoria a todas, todos los interesados en participar de los Talleres Lúdico-Matemáticos (Google Classroom) de nuestro Círculo Matemático Kimche, que realizamos todos los días lunes de 18:00 a 19:00hrs, con excepción de feriados, recesos académicos. 

Interesadas, interesados pueden inscribirse mediante el formulario (2-2021)  (Menores de edad solicitar Consentimiento Informado a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.)

Mirar a través de lentes la mayoría de las veces nos permite recobrar nuestra visión en detalles, texturas, pero también quizás nos 'aumenta' y reafirma en nuestras creencias de como pensamos que es el mundo a nuestro alrededor. Como Mafalda, si nos probamos los lentes equivocados podemos distorsionar la realidad peligrosamente, entonces, ¿Qué lentes nos ayudan a mirar con precisión este mundo, dinámico y en constante transformación? Desde aquí pensamos que unos lentes matemáticos son una buena alternativa! nos aportan una perspectiva común y compartida por todas y todos, son una buena prescripción.

Quienes han leído la bella obra literaria El Principito, cuando éramos niña, niño, adolescente o bien edad adulta, siempre nos invita a pensar en la importancia del dialogo tomando en cuanta distintos puntos de referencia, desde donde muchas veces  miramos las cosas que nos rodean y que nos importan:

- Me encantan las puestas de sol. Vamos a ver una puesta de sol...

- Pero hay que esperar...

- Esperar qué ?

- Esperar a que se ponga el sol.

Primero pareciste muy sorprendido, y luego te reíste de ti mismo. Y me dijiste:

- Siempre creo que estoy en casa !

En efecto. Cuando es el mediodía en Estados Unidos, el sol, como todo el mundo sabe, se pone en Francia. Bastaría poder ir a Francia en un minuto para asistir a la puesta del sol. Lamentablemente, Francia está demasiado alejada. Pero en tu planeta tan pequeño, te alcanzaba con correr tu silla algunos pasos. Y mirabas el crepúsculo cada vez que lo deseabas...

Cuando miramos a través de un lente vemos mas que simples imágenes. Nuestros ojos son un filtro geométrico que nos proyecta en el mundo exterior, ¿Cuál es la geometría que esta fuera de nuestros sentidos? Dejamos algunas imágenes para provocar nuestra imaginación que nos libera desde las limitaciones de nuestros sentidos!

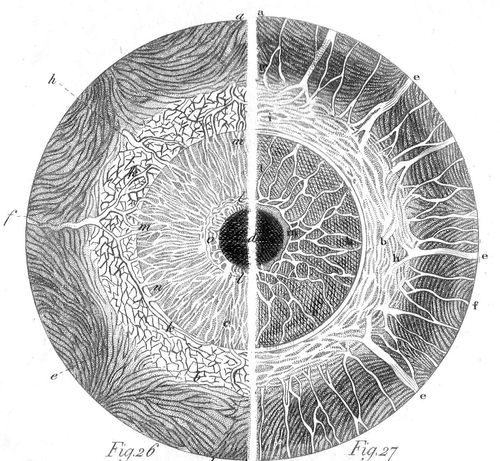
Nuestro lente, aquel lente que esta incorporado en nuestro cuerpo, son los ojos, diseñados en función a la evolución de nuestra especie, esculpido minuciosamente desde nuestras capacidades y actividades pedestres. 

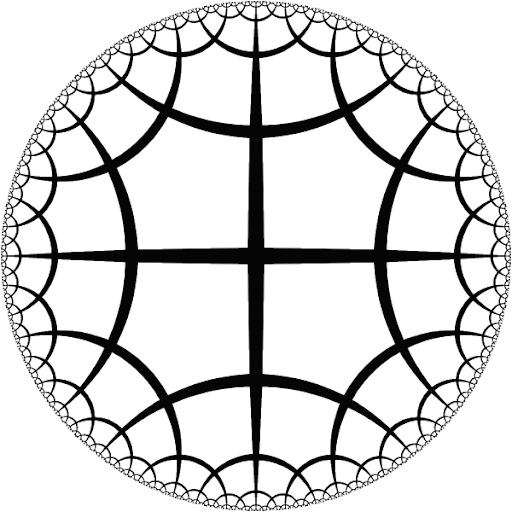
Las geometrías no clásicas (Disco de Poincaré), aquellas que nacieron de la imaginación a partir de refutar el quinto postulado de Euclides, nos dan pistas de las cosas no necesariamente habitan lo cartesiano!  

A veces nuestro visión se pierde, se gasta, mirar en detalles no es lo mismo con el pasar de los años, entonces, echamos manos a lentes ópticos, ajustados y prescritos a los defectos mecánicos singulares, recuperamos aparentemente la precisión de la vista una vez perdida, pero algo sucedió, miramos a través de otros lentes, un filtro, un nuevo interprete de la realidad.

Y quizás, aquellos ángulos no son los mismos que alguna vez vimos, ya no suman 180°, ya no hay paralelas.... habitamos en otra geometría (Circle Limt I, M.C. Escher).

'Objects in mirror are closer than they appear' (Vista Ojo de Pez)

Nos encontramos celebrando a nivel institucional el Mes de los Pueblos Originarios oportunidad también de celebrar el año nuevo del hemisferio sur, el Wetri pantu. Esta no es la primera vez que proyectamos este documental desde nuestra organización, que es el registro que nos inspira tras el Círculo Matemático Navajo, uno de los primeros círculos matemático indigenistas del mundo. Esperamos sin embargo, convocar a mas actores y actrices desde la comunidad universitaria, académico y local.

En este esfuerzo se suman el Cine Club ULagos, la carrera de Pedagogía en Matemática y Computación ULagos

Estuvimos este sábado 22 de mayo compartiendo con el equipo de 'Démosle vuelta, café con mate' espacio de conversación que en esta segunda oportunidad nos invito a compartir reflexiones, experiencias de vida, visiones y ciertamente el trabajo que hacemos aquí, que no inspira, que nos motiva. Si deseas conocer la entrevista en extenso puede escuchar en el canal de spotify o bien verla en el canal de youtube.

Gracias por pensar en Círculo!

#mateconcafechallenge (Carlos Martínez)

Desde la literatura, pero también desde el cancionero popular nos encontramos con historias que nos permiten reflexionar sobre nuestra condición humana, compartiendo elementos, ideas que nos interpelan desde distintas sensibilidades. Es así como vemos que en la canción de Silvio Rodríguez, Fabula de Tres Hermanos, el cantautor no sólo nos ofrece una fabula, sino también una paradoja:

Fabula de Tres Hermanos

Silvio Rodríguez

Por esto días nos encontramos con un cortometraje llamado 'Alternative Math' (Matemática Alternativa), que pone en debate en sus pocos minutos muchas temáticas alrededor de la idea de que la matemática está formada por verdades incuestionables, de allí se desprende el rol de las, los profesores en la administración de estas verdades en un contexto social y cultural donde prima lo políticamente correcto, es decir, evitar a través del lenguaje, nuestra comunicación ofender, poner en desventaja a personas de grupos particulares de la sociedad. El debate entonces queda entre la contraposición de una verdad matemática incuestionable, y si esta puede ponerse en entredicho, y si quien lo haga está en un error.  

'2+2 = 4 y no es 2+2 = 22' (Quizá.. si)

¿Cuál es nuestra postura? Pues bien, entendiendo que, en el rol de una, un profesor especialmente en los niveles tempranos de un sistema de educación está formando personas y enseñando conceptos básicos fundamentales, podríamos conceder que debe presentar la verdad matemática con una intensión de rigor, precisión, pero no debe excluir la reflexión crítica-creativa propia que es una característica del quehacer de la disciplina. El desafío es disponer de la mejor respuesta para una niña, niño curioso y asertivo. En el efecto social desencadenado alrededor de la decisión de la profesora por defender la verdad matemática como monolítica por la que se enfrentó al escarnio público, quizá se deja entrever una crítica al modelo cultural de lo políticamente correcto y que en el argumento se tensiona sobre cuál es su límite, esto escapa de lo que podemos responder aquí, pero creo que es un buen principio a considerar en nuestro quehacer diario, teniendo presente que esta forma de ser no se contrapone ante la verdad científica.  Por último, e igualmente inquietante, la tesis de que '2+2=4' es una verdad monolítica, merece algo más que la postura de la profesora, sabemos que esto puede ser reinterpretado de múltiples maneras en matemática, algo así como en reflexionar sobre cuantas formas de 'igualdad matemática' existe.

Este lunes 12 de Abril iniciaremos nuestro ciclo de talleres, esta vez en formato virtual tratando de superar las restricciones producto de la pandemia. Ha sido una apuesta, que confiamos que será exitosa y con la que podremos llegar a niñas, niños y jóvenes de la provincia de Osorno y sus alrededores. antes de comenzar debemos recordarles algunos detalles técnicos para poder participar.

Herramientas:

1. Videoconferencia: ZOOM (Disponible para instalación smartphone, computador)
2. Google Classroom: Como plataforma de comunicación, materiales (Requerimiento cuenta gmail.com)

Durante la primera sesión de este lunes 12 de abril, realizaremos las orientaciones fundamentales del cómo utilizaremos estas herramientas y compartiremos una primera actividad como ejemplo.

Agradecemos compartir, difundir el formulario de incorporación requisito para participar!

Formulario de Incorporación 2021

Nos vemos con nuestro mejor ánimo y disposición!

¿Simetría no sólo es un concepto matemático..? una cosa es cierta para comenzar, es un fenómeno presente en nuestra percepción del mundo que nos rodea, es una manifestación de nuestros sentidos y como a partir de ellos se representa esta realidad en nuestro cerebro, el corazón de la maquina inteligente que decimos ser. 

La Real Academia Española nos aporta con:

simetría

Del lat. symmetrĭa, y este del gr. συμμετρία symmetría.

1. f. Correspondencia exacta en forma, tamaño y posición de las partes de un todo.

2. f. Biol. Correspondencia que se puede distinguir, de manera ideal, en el cuerpo de una planta o de un animal respecto a un centro, un eje o un plano, de acuerdo con los cuales se disponen ordenadamente órganos o partes equivalentes.

3. f. Geom. Correspondencia exacta en la disposición regular de las partes o puntos de un cuerpo o figura con relación a un centro, un eje o un plano.

En cualquiera de las acepciones, aparece la palabra ‘correspondencia’, que podríamos interpretarla para nuestra nota, algo así como, ‘un mapeo uno a uno entre dos partes, objetos’. Extrapolando de esta idea, lúdicamente por su puesto, podemos también situar la simetría en contextos y convenciones sociales, e inclusión como parte de principios de la psicología. 

En el marco de las Leyes de la Gestlat, se encuentra el principio de simetría, que reafirma que esta propiedad es el resultado de nuestro sistema perceptivo. 

‘Las imágenes simétricas son percibidas como iguales, como un solo elemento, en la distancia. Este principio tiene tal trascendencia que va más allá del campo de la percepción de las formas y constituye uno de los principios o fenómenos fundamentales de la naturaleza. La biología, la matemática, la química y la física, incluso la misma estética, se organizan siguiendo las leyes especulares, simples o múltiples, de la simetría.’

Invocamos ‘simetrías’ en las relaciones humanas a diario, derechos humanos y sociales, reivindicaciones de género, en el trato, en como distribuimos los recursos, en fin, da la impresión de que esta percepción de nuestros sentidos nos gobierna de alguna manera para promover y representar un orden de affaires sociales con un sentido de justicia. Con algo más de certeza podemos decir que ‘Simetría’ no es sólo un chiche geométrico

Este próximo 14 de marzo, se conmemora el día internacional de las matemáticas, fecha instaurada en la Resolución 30 del año 2019 por la UNESCO, en que se señala:

‘'Una mayor conciencia mundial y un fortalecimiento de la enseñanza de las ciencias matemáticas son esenciales para hacer frente a desafíos que se plantean en ámbitos como la inteligencia artificial, el cambio climático, la energía y el desarrollo sostenible, y para mejorar la calidad de vida en el mundo desarrollado y en el mundo en vías de desarrollo. '

 Este enunciado es un reconocimiento a la importancia transversal de esta disciplina en el desarrollo cultural y científico de la humanidad. Este año, la consigna es ‘Matemáticas para un mundo mejor’, la que es amplia y profunda, ya que esta aspiración por un ‘mundo mejor’ es multidimensional, diversa, polisémica, cubriendo desde el buen vivir, medioambiente, relaciones humanas.

 Cabe preguntarse entonces de que manera el cultivar esta disciplina, no sólo desde la creación, descubrimiento en la frontera científica, sino de la experimentación, la actividad lúdica, creativa, dialógica cotidiana podemos aspirar a un mundo mejor. La respuesta es mas evidente de lo críptico que pueden ser las matemáticas para muchas, muchos a priori, pasa por disponerse a compartir, en asumir desafíos, a atreverse a resolver problemas, mejor aún si esta actividad académica y/o lúdica la realizamos con otras y otros.

 La invitación para este día 14 de marzo es conectarse con tantas actividades que se realizarán alrededor del mundo a través de las redes sociales y web en general. Compartir la aventura por aprender algo nuevo, es un primer paso en la búsqueda de un mundo mejor.

Carlos Martínez Méndez

Coordinador Académico

Círculo Matemático Kimche

Conmemoraremos el Dia Internacional de las Matemática 2021, instituido por la UNESCO, y que este año lleva por consigna 'Matemáticas para un mundo mejor'. Como acto conmemorativo proyectaremos, siendo el estreno en Chile y Hispanoamérica, el documental 'Math Circles around the world' de la realizadora Ekaterina Eremenko, quien tiene una larga trayectoria documental, destacando afamados títulos como 'Color of Math (2012)' que es el testimonio de notables matemáticas/cos en vida como los medallitas Fields  Cedric Vilani and Maxim Kontsevich.

En esta oportunidad Ekaterina registra los testimonios tanto de niñas, niños, jóvenes participantes en círculos matemáticos alrededor del mundo, así como académicas, académicos que los organizan

Referencia: Ekaterina Eremenko Films - Math circles around the world (Trailer)

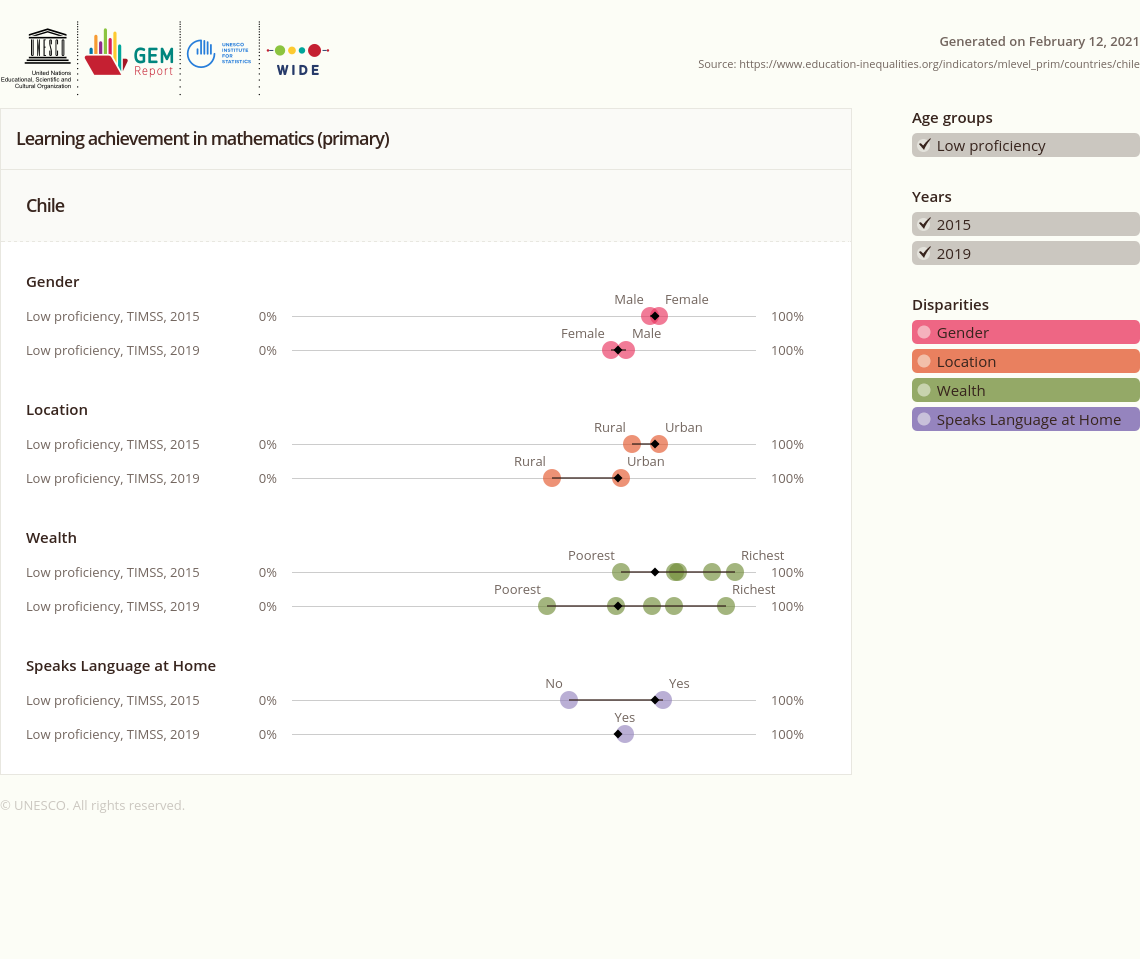
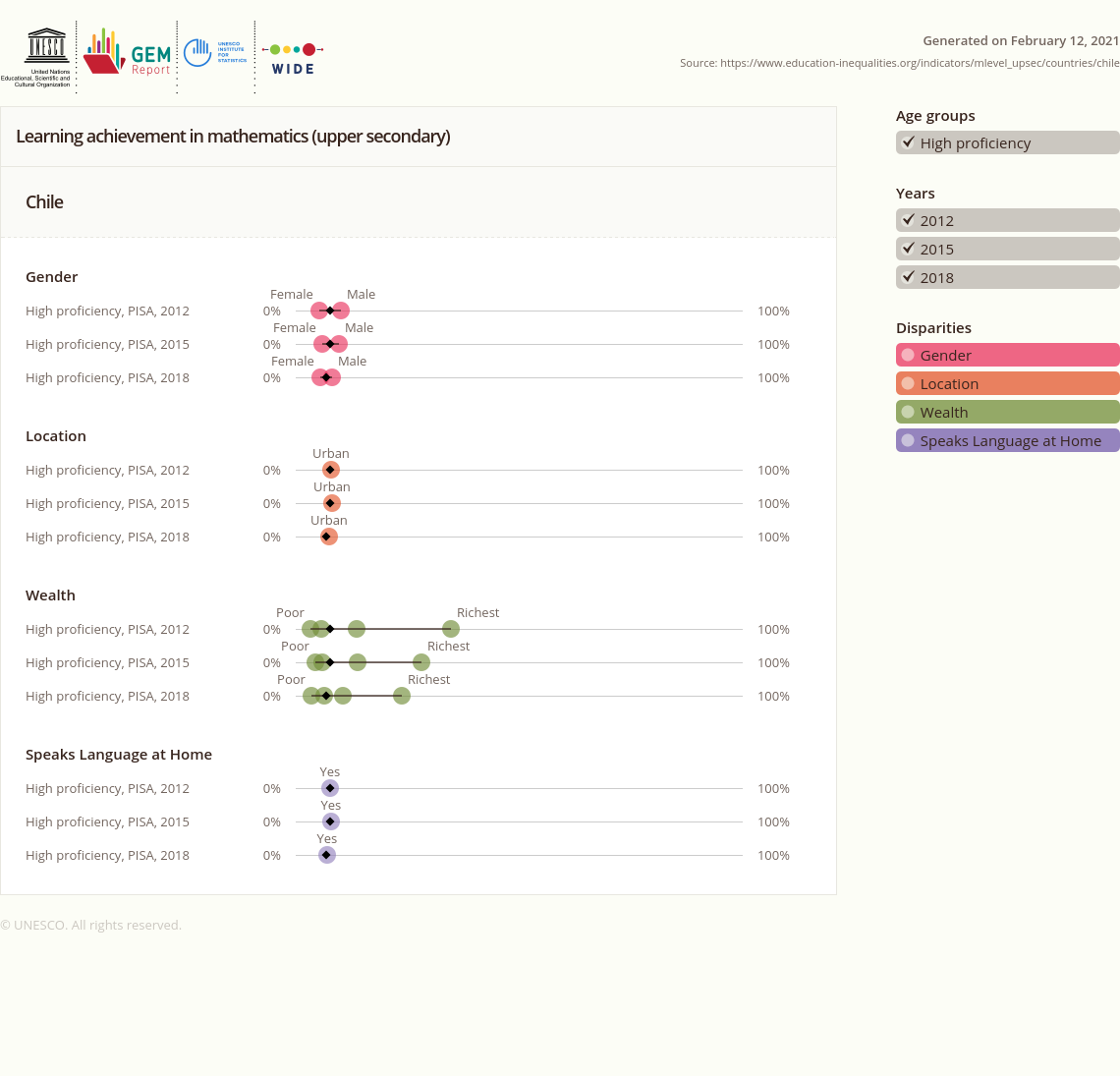
Los desafíos existentes en muchas dimensiones, tal como se definen las Naciones Unidas en sus Objetivos de Desarrollo Sostenible, equidad es uno central y de escala global. Si ponemos atención en esta dimensión desde la enseñanza de la matemática (Primeria TIMMS, Secundaria PISA) en Chile, veremos que hay mucho por avanzar, si además relacionamos el desempaño en estos test globales que miden las habilidades, capacidades y contenidos de esta disciplina, con otras dimensiones importantes tales como, distribución territorial, étnica, género, y social, veremos que los desafíos se multiplican. 

Compartimos algunas de las estadísticas que dispone la UNESCO (World Inequality Database on Education) sobre distintas dimensiones de la educación a nivel mundial. Las imágenes siguientes nos describen algunos aspectos de la realidad chilena: 

Niveles de Logro (Más bajos) en Educación Básica (TIMMS 2015-2019), intersección : Género, Localidad, Riqueza, e Idioma.

Niveles de Logro (Más bajos) en Educación Media (PISA 2012 - 2015- 2018), intersección : Género, Localidad, Riqueza, e Idioma.

Permanencia en Educación Superior por Regiones (Los Lagos versus Metropolitana )intersección :  Género, Riqueza.

En cada nivel educacional emergen marcadas brechas en el desempeño de las, los estudiantes en estos test globales, así como en la preminencia en Educación Superior, donde la pobreza, ser mujer, vivir en la ruralidad y estar en regiones constituyen condiciones adversas. No olvidemos también para quienes se reconocen como parte de un pueblo originario: Aymaras, Collas, Diaguitas, Mapuches, Huilliches en otros, los efectos son mas severos.

¿Cómo podemos hacer frente a las desigualdades de oportunidades en educación? Nosotros confiamos en que  cultivar valores y principios en el día a día, tales como respecto, jubilo, compromiso, trabajo colaborativo son algunas de las herramientas que disponemos para enfrentar las brechas que ofuscan el buen vivir que todas, todos necesitamos con urgencia, esto es lo que somos! Miramos el mundo con otros ojos!

Por esto días escuche la presentación de Premio Nobel de Física, Kip Thorne, quien fuera 'Profesor Feynman de Física Teórica' del Instituto Tecnológico de California (CalTech) , como parte del Congreso Futuro 2021 (Vídeo Disponible) y titulada “Podemos entender las leyes físicas del universo como si fueran Dios” oportunidad donde entrega detalles de su estrecha colaboración con el cineasta Christopher Nolan durante la producción de la  película de ciencia ficción 'Interstellar', que es un potente ejemplo como desde distintos ámbitos del conocimiento, las expresiones tanto de la creación científica, como artísticas se nutre y entrelazan. 

Este es un ejemplo, que invita a reflexionar sobre los alcances de acciones transdisciplinares, donde ésta interacción se entiende como estrategias de investigación más allá de las fronteras disciplinares, definiendo así enfoque holísticos entorno a la resolución de problemas. En este sentido, creemos que la reflexión y la búsqueda de estos enfoques holísticos es propio del séptimo arte, o como enunciamos coloquialmente el arte de las siete artes. En una película, emergen, la imagen, el guion, la escenografía, las artes escénicas, todas expresiones de las artes, pero como bien lo testimonia Thorne, las ciencias no están excluidas de su repertorio conceptual y técnico. Entonces, ¿El séptimo arte dialoga con las ciencias exactas? pues si, categóricamente, si!

Dejamos algunas recomendaciones para 'Mirar este mundo con otros ojos' la próxima película que veas.

1. Articulo Diario El País (España) 'Cine y matemáticas: Las matemáticas aparecen cada vez con más frecuencia en el cine, pero a menudo se ofrece de ellas una visión distorsionada y sensacionalista'
2. Libro 'Matemática y Cine ' JM Sorando 

Algo nos dice que en los tiempos atribulados que estamos viviendo, requerimos con urgencia un nuevo horizonte, un nuevo fin común que nos permita movilizarnos teniendo presente el bien común, condición que nos define como seres humanos. Incerteza es quizá la mejora palabra para describir estos tiempos, reclusión, contagio, cambios a nuestro pacto social, desafíos medioambientales, responder a las brechas culturales y de género, dar frente a las segregaciones sistémicas, producto  de un mercantilismo sin limites. ¿Qué podemos hacer? Individualmente, creemos que no hay opciones por esta vía, quizá desde lo gregario hay más posibilidades, sólo queda explorar nuevos senderos que nos propicien cambios culturas, nuevos tratos a todo nivel y escalas.

Deseamos compartir algunas reflexiones con el animo de provocar, de motivar a la acción por el cambio, pero en esta primera visita a este importante tema queremos hacerlo con una palabra:

Eudaimonía (griego: εὐδαιμονία /eu̯dai̯moníaː/) es un término griego comúnmente traducido como felicidad, bienestar o vida buena; también se ha propuesto "florecimiento humano" o "prosperidad" como su traducción más precisa

Pronto retomaremos este tema en profundidad!

Con el propósito de empaparnos de todo lo que pudimos echar mano, durante el pasado 6 al 9 de enero asistimos virtualmente al mayor congreso de matemática y educación matemática que se realiza en los Estados Unidos, El 'Joint Mathematics Meetings 2021' que esta versión se realizo de manera virtual gracias a una robusta plataforma de conexión y ZOOM. Este congreso se caracteriza por disponer tanto de sesiones plenarias, sesiones temáticas y exposiciones tanto de herramientas, software, casas editoriales, y también artes, todo lo que se mantuvo en esta versión virtual en atención a la pandemia que nos afecta. En general la moral de los participantes fue increíble, alta participación, no solo desde los Estados Unidos, si no también de otras partes del mundo como nosotros.  

Por nuestra parte pudimos asistir a seccionales por un lado de Historia de la Matemáticas, Inclusión-Género-Minorías Éticas, por otro, seccionales de Lógica Matemática, así como un panel de discusión sobre la docencia universitaria en matemática en contexto de pandemia. Por último, participamos como parte del jurado de una sección de poster en Álgebra, donde pudimos apreciar el alto estándar de estudiantes de pregrado y secundaria que gracias al patrocinio de una, un académico abordaban temas de investigación de frontera.

Una comunidad para todas y todos!

Este próximo jueves 14 de Enero se celebra el tercer día internacional de la Lógica, fecha que coincide con el día del fallecimiento del afamado lógico-matemático austro-húngaro Kurt Gödel. La Lógica es considerada como la ciencia del razonamiento formal, es aquella disciplina que se preocupa sobre el sentido riguroso de verdad, discute por tanto todos los aspectos que permiten hacer sentido de este importante concepto, también reflexionar de los limites de los sistemas formales con que modelamos la verdad formal. Por otro lado, culturalmente la lógica está en el centro de todo lo que nos permite regular nuestras convenciones, acuerdos, toma de decisiones, sin un sentido de lo que es correcto, nada tendría sentido en nuestras relaciones sociales.

Es oportuno por tanto, reconocer la importancia cultural de esta disciplina que ha sido fundamental a lo largo de la historia de la humanidad y de la construcción del conocimiento científico, humanista  que hoy conocemos, manteniendo su importancia y vigencia siendo el motor del avance tecnológico que hoy en día toma múltiples formas,  esta el corazón del advenimiento de las maquinas inteligentes, la web,, es decir, de la inteligencia artificial que esta transformando lo que hoy conocemos en medio de una quinta revolución industrial.

Nuestros honores a esta bella disciplina! que permea la Filosofía, Matemática y Ciencias de la Computación donde se expresan sus ramificaciones más notables!

Bonus track: Vida y obra de Kurt Godel (Sandra Takano) y  el primer día de la lógica (Lógica Universalis)

Con lo años aprendemos a reconocer el largo y arduo camino de la 'iluminación',  del conocimiento. Es interesante reconocer que no existen atajos, a pesar de los espejismos, aquellos que nosotros mismos nos creamos a lo largo del camino, muchas veces pensamos que poseemos una verdad, pero al dejar pasar unos minutos, se vuelve a escapar de nuestras manos. Podríamos también creer en que este camino de iluminación es individual, sin embargo, es más colectivo de lo que a primera vista podemos pensar. El conocimiento es un intangible que es una obra colectiva, sean científicos, humanistas, artistas, cada una, uno de los participantes de esta obra, pone un nuevo ladrillo, o página, o libro en la construcción de la Gran Biblioteca de Babel, es este contexto colectivo en que la persuasión dialógica es la mejor herramienta para medir cuanto sabemos realmente de algo.

¿Qué podría sucedernos si no sometemos lo que sabemos con los demás? (El efecto Dunning-Kruger)

La naturaleza es un pozo sin fondo de cosas que provocan nuestra reflexión como seres humanos, la imaginación comienza desde la diversa realizada de cosas, formas, colores con que nos estimula y despierta nuestra emociones. 

Compartimos dos imágenes, una proveniente desde la naturaleza, donde se observa un mecanismo de defensa de un colmenar natural (Apiario), donde miles de abejas de manera sincronizada 'hacen olitas' diseñando patrones que dan la impresión de que el colmenar es un animal, una unidad y que utiliza como mecanismo de defensa. Por otro, una imagen gif donde se muestra el recorrido puntos sobre un disco siguiendo las rectas de la geometría hiperbólica del disco (Poincaré) . Ambas imágenes en su dinámica tiene algo, un que se yo, común ¿No?

Esta semana se realizo la premiación del concurso literario 'Matemática y Computación en 314 palabras' a pesar de la pandemia, de las dificultades, del cansancio, estrés llegaron relatos desde distintas localidades de Chile. Esta fue una primera experiencia, que esperamos repetir y seguir perfeccionando, aportando a la valoración de estas ciencias que son sustento del presente y futuro próximo. Compartimos los premiados de esta versión 2020.

Premiación del Concurso 'Matemática y Computación en 314 palabras' 

 Primer Lugar

(Puerto Montt, Región de Los Lagos)

Felicitaciones a los ganadores, y la invitación que da extendida para la próxima versión!

George Polya (Natalicio, 13 de Diciembre) fue un matemático del siglo pasado, académico del Departamento de Matemática de la Universidad de Stanford, formador de generaciones de matemáticas, matemáticos, 31 estudiantes doctorales y una descendencia académica de cerca 250 académicos en esta disciplina. Contribuyó no tan solo a la matemática, si no también, quizá sin planificarlo, desde su afamado libro 'How to Solve it' (¿Cómo resolverlo?) (1945) delineo lo que vendría llamarse 'resolución de problemas' que tiene múltiples ramificaciones tanto en la psicología, ciencias cognitivas, computación, lógica entretantos otros campos y disciplinas.

Resolución de Problemas según Polya

1. First, you have to understand the problem. (Entender)
2. After understanding, make a plan. (Estrategia)
3. Carry out the plan. (Ejecutar Estrategia)
4. Look back on your work. How could it be better? (Revisión - Reflexion - Mejora)

 Entendemos que esta visión original sigue siendo valida al día de hoy, pero ha sido enriquecida fuertemente por la integración de visiones de distintos campos disciplinares, poniendo el acento también en los aspectos socio-emocionales de la resolución de problemas. 

Nuestro compromiso es profundizar este paradigma de la apropiación, vivencia de la experiencia creativa que es la matemática

Durante esta semana hemos participado de las actividades organizadas por el equipo de la Dirección de Acceso, Equidad y Trayectoria en que nos hemos reunido con estudiantes interesados(as) en conocer nuestra propuesta curricular de la Carrera de Pedagogía en Educación Media en Matemática y Computación. En esta ocasión preparamos una presentación de dos tiempos, una primera parte en que nos concentramos en presentar el proyecto educativo y una segunda parte donde proponemos una reflexión sobre la importancia de la matemática en el quehacer humano desde los científico, cultural y social. A continuación compartimos tanto la presentación y el vídeo de la segunda parte de esta satisfactoria jornada.

Presentación PMYC-Experiencia Disciplinar 2020 (Octubre)

Video: 'Matemática en todas las cosas'

Con alegría estaremos en la Charla del Profesor Japheth Wood, quien a liderado importantes iniciativa en el ámbito de los Círculos Matemáticos! Es una buena oportunidad para conocer estos esfuerzos que recientemente fueron reconocidos por la AMS.

Desde la UNESCO (United Nations Educational, Scientific and Cultural Organization) se establecen recomendaciones en un amplio sentido de la educación en todos sus niveles y ámbitos disciplinares, es así como Aportes para la enseñanza de la matemática (2016) a partir de este informe se desprenden directrices sobre los conocimientos, destrezas, capacidades, habilidades, principios, valores y actitudes  fundamentales en el ámbito de la educación matemática que adscribimos plenamente. Destacamos algunos pasajes significativos de este informe elaborado por un equipo interdisciplinario que incluye destacados académicos chilenos:

'La resolución de problemas da la posibilidad a los estudiantes de enfrentarse a situaciones desafi  antes que requieren para su solución variadas  habilidades, destrezas y conocimientos que no siguen esquemas fi jos. Estas incluyen el cálculo numérico escrito y mental, las nociones espaciales, el análisis de datos, el uso de herramientas matemáticas y las estimaciones, entre otras. Nuevamente, se explicita la relevancia del rol que cumple el docente: otorgar a los estudiantes instancias para poner en práctica estas habilidades y, al mismo tiempo, brindarles experiencias que los ayuden a comprender que la matemática es más que una aplicación automática de una cantidad fi  nita de procedimientos (Peng Yee, 2014)'  (Extracto pág  27 Aportes para enseñanza de la Matemática)

Durante el segundo semestre participaremos de la oferta docente del Centro de Formación Integral con la asignatura 'Ludomática: Una introducción a la Matemática Recreativa' en que esperamos plasmar nuestros años de experiencia en el ámbito de la educación de la matemática no sólo con un fin formal y académico, si no como una experiencia de vida, lúdica y creativa!

Reseña Curso:

Recientemente se publico una nota en el diario español El País titulada 'El matemático que afirma que pi no es un número' Doron Zeilberger es bien conocido por sus contribuciones a la combinatoria y también por sus opiniones controvertidas, ¿Sigue siendo un debate matemático? Quizá parece obvio, pero el fondo de debate es profundo y vuelve sobre la idea de infinito que ha penado a las mentes brillantes de la matemática por siglos de los siglos, infinito es una cantidad, o es una idea concepto abstracto que sólo habita el universo de los platonismos, pues bien, hay quienes que afirman que sólo existe lo finitamente grande y la capacidad de lo que es algorítmicamente asequible.

Reseña de la nota:'Más allá de algunas manías muy loables sobre horarios y uso de teléfonos móviles y ordenadores en los seminarios científicos (en concreto, defiende que no se deberían usar las charlas como excusa para revisar el correo electrónico personal), su convicción más singular es que se adhiere al ultrafinitismo, una negación severa del infinito “puro” matemático. Esta doctrina va en la línea de una corriente de la filosofía de las matemáticas llamada intuicionismo, más conocida y menos extrema. En términos prácticos, Zeilberger considera que solo tiene sentido aquello que es algorítmicamente construible.'

Cuando caminamos a lo largo de un puente, muchas veces no miramos el arte de su construcción, tensiones, cables que sustentan y dan estabilidad a la estructura en su conjunto ¿Logras identificar algunas de la curvas de la imagen?

Semanas y semanas de cuarentena, cerco, distanciamiento social, todo para evitar las consecuencias de una epidemia sin control. La única respuesta es paciencia, y retomar tiempo para aquellas cosas que nos den tranquilidad espiritual.... En el parque podemos encontrar algo de geometría para dejarnos llevar por la simetría y belleza de estas ideas

Nuestra misión continua, estamos trabajando paso a paso, para contar pronto con los medios de conectividad mínimo para volver a reunirnos desde espacios virtuales, las actuales circunstancias a pesar de los difícil y alarmantes no demandan mantener nuestro espacio lúdico-matemático más allá de las aulas y las reuniones regulares. Por ahora pedimos paciencia, esperamos pronto estar en condiciones de reuniones en la red con ustedes!

Algunas recomendaciones antes de comenzar:

Un año más en la cuenta de Pi (En inglés Pie=Pastel), el día de conmemoración es el 14 de marzo (En inglés march 14th = 3/14) , desde donde podemos ver la aproximación '3,14' de este número irracional famoso. Por primera vez se celebro el año 1988 en la ciudad de San Francisco en los Estados Unidos, luego en el año 2009 la Casa de Representantes de los Estados Unidos declaro este día como el 'Día de Pi', el año pasado la Unesco declaro este día como el día internacional de la matemática.

Pi no es un número más, es una constante que aparece una y otra vez en la naturaleza, y sin duda, juega un rol central en un sin fin de áreas de la matemática pura y aplicada. Los primeros que se enfrentaron a su existencia fueron matemáticos y geómetras egipcios, griegos, babilónicos, chinos entre otros muchos. Algunos destacaron por su mayor precisión y belleza de argumentos, por ejemplo Archimedes  concibió un algoritmo de aproximaciones sucesivas del círculo mediante polígono regulares, construcción que es una expresión de la belleza del pensamiento matemático. Este algoritmo representa un proceso infinito convergente, algo que para esa época generaba conflictos filosóficos, tiempo en que se niega, desecha la idea de infinito como contra-intuitiva, a pesar de ello persistió a través de una idea alterna, 'tan grande como sea posible' que es la esencia de lo que muchos siglos mas tarde sería concebido como convergencia analítica de sucesiones. 

En fin, como decíamos, este número nos alimenta día a día de acertijos e inspira nuevas mentes brillantes hacia el trabajo matemático, es todo un honor ser el símbolo que celebra la matemática en todo el mundo!

Participamos y aportamos nuestra visión desde instancias culturales y educativas no formales. Compartimos nuestro mensaje de que el aprendizaje cooperativo están importante como el aprendizaje individual, y que la matemática y su ejercicio no solo contribuyen a materias y habitabilidades cognitivas, si no también a cultivar habilidades sociales!

Creemos necesario pronunciarnos sobre los acontecimientos que estamos viviendo como país a lo largo y ancho de nuestro territorio. Para nosotros es un momento de congoja ver el nivel de incertidumbre en que nos encontramos y como día a día mucha de las expresiones que dominan la agenda se alejan del entendimiento mutuo. Desde el día que comenzamos nuestro trabajo nos abocamos a la tarea de promover un espacio de acercamiento, amistad y complicidad por participar de sesiones de dialogo en que la tarea de cada día fuese asumida por todas, todos quienes estuviesen presentes, es el sentido de lo que hacemos, dialogar, reflexionar y resolver problemas con la participación de cada uno de los participantes.

Siempre es una agrado que nos entrevisten y que nos pregunte por lo que hacemos! escuchamos!

Con el mismo entusiasmo estuvimos promocionando nuestra jornada para el próximo Viernes 18 de Octubre desde la radio de nuestra casa, La radio Universidad de Los Lagos aquí en Osorno. Los esperamos!

Resolución de problemas es un área de investigación de la didáctica matemática que esta en constante evolución. El primero en acuñar el concepto de resolución de problemas fue el matemático de origen hungaro George Polya quien define la resolución de problemas como un proceso reflexivo que tiene etapas definidas como sigue:

Resolución de Problemas según Polya

• Entender el problema
• Definir una estrategía de solución
• Ejecutar la estrategía de solución
• Examinar la solución

La etapa de la compresión de un enunciado es clave en la consecución de la solución del problema, es aquí en el primer paso de este proceso que muchos de los errores y horrores suceden, replatear la pregunta y reconocer la información e hipotesis sobre las cuales desarrollaremos la solución del problema, parece muchas veces lo más facil de la tarea de la resolución de  un problema, sin embargo, esta etapa esta estrechamente relacionada con los preconceptos, las sensibilidades y experiencias de cada uno de nosotros. Compartimos una capsula que consiste de una secuencia de test orientadores de como abordar esta etapa crucial, este trabajo fue elaborado por un equipo académico y de soporte técnico comprometido bajo el fin de desarrollar las habilidades matemáticas entre estudiantes de ingreso a nuestra universidad. El resultado y pilotaje arrojo resultado promisorios!

LINK: Cápsula de Resolución de Problemas (ULAGOS+KIMCHE)

El Círculo Matemático Kimche inicia una nueva convocatoria de inscripciones para participar de nuestros tradicionales talleres lúdicos matemáticos que realizaremos los diás martes desde las 17:35 hrs - 19:00 hrs en el laboratorio de matemática y computación en el segundo piso del pabellón E, Campus Chuyaca, Universidad de Los Lagos, Osorno.

 La invitación es a registrarse vía correo electronico Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.